Correção de LP e demonstração por indução, por Ted Sider

Tradução de L. H. Marques Segundo

[…] Consideramos as abordagens sintática e semântica para a lógica proposicional (LP). Em cada caso, introduzimos as noções formais de verdade lógica e consequência lógica. Na abordagem semântica essas noções envolveram a noção de verdade em interpretações de LP. Na abordagem sintática, consideramos duas definições formais, uma envolvendo demonstrações por sequentes, e outra envolvendo demonstrações axiomáticas.

Que complicação! Temos múltiplos tratamentos formais para as nossas noções lógicas. Mas de fato, pode-se mostrar que todas essas três definições produzem exatamente os mesmos resultados. Provarei isso aqui apenas para a noção de um teorema (a última linha de uma demonstração axiomática) e para a noção de uma fórmula válida (verdadeira em todas as interpretações de LP). Farei isso provando as duas seguintes proposições:

Correção de LP: Todo teorema de LP é válido em LP.

Completude de LP: Toda fbf válida de LP é um teorema em LP.

A correção é bastante fácil de provar; faremos isso num instante. A completude é mais difícil, e a provaremos na seção 2.9. A correção e a completude conjuntamente nos dizem que a validade e a teoremicidade em LP coincidem exatamente.

Mas primeiro um breve desvio: precisamos introduzir um método de demonstração que seja ubíquo na metalógica (como é na matemática geralmente): o método da indução. A ideia básica, em sua forma mais simples, é esta. Suponha que temos infinitamente muitos objetos enfileirados, assim:

E suponha que queremos mostrar que cada um desses objetos tem certa propriedade. Como fazer isso?

O método da indução nos faz proceder em dois passos. Primeiro, mostrar que o primeiro objeto tem a propriedade:

Isso é chamado de “caso de base” da demonstração indutiva. Depois, mostramos que quando algum dos objetos na linha tem a propriedade, o próximo objeto na sequência também a tem. A isso chamamos “passo indutivo” da demonstração. O método de indução diz que: se você estabeleceu essas duas coisas, você pode ir adiante e concluir que todos os objetos na sequência têm a propriedade. Por que essa conclusão é justificada? Ora, uma vez que o primeiro objeto tem a propriedade, o segundo tem também de ter a propriedade dado o passo indutivo:

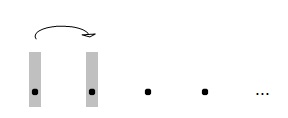
Mas então outra aplicação do passo indutivo nos diz que o terceiro objeto tem também a propriedade

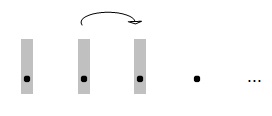
E assim por diante; todos os objetos na sequência têm a propriedade:

É assim que a indução funciona quando aplicada a objetos enfileirados da maneira ilustrada: há um primeiro objeto na sequência; depois de cada objeto há exatamente outro objeto; e cada objeto apresenta algum número finito de salto após do primeiro objeto. A indução pode também ser aplicada a objetos estruturados de diferentes modos. Considere, por exemplo, a seguinte grade de objetos:

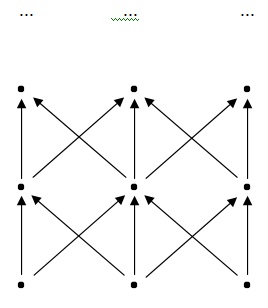
Na base dessa grade há três pontos. Cada par desses três pontos se combina para produzir um novo ponto. (Por exemplo, o segundo ponto da extrema esquerda de baixo pra cima é produzido pelos dois pontos da esquerda da base). Os três pontos resultantes (formados a partir dos três pares obtidos dos três pontos da base) formam o segundo nível da grade. Esses três pontos do segundo nível produzem o terceiro nível do mesmo modo, e assim por diante. Suponha, agora, que se poderia provar os três pontos da base têm alguma propriedade:

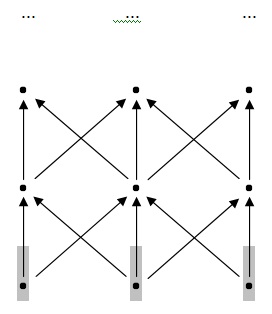
(Esse é o caso de base). E suponha também que se poderia provar que quando dois pontos com a propriedade se combinam, o ponto resultante também tem a propriedade (passo indutivo). Então, assim com no exemplo anterior, a indução nos permite concluir que todos os pontos na grade têm a propriedade. Dado o caso de base e o passo indutivo, sambemos que os pontos no segundo nível da grade tem a propriedade:

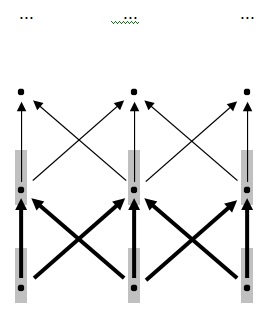
Mas então, dado o passo indutivo, sabemos que os pontos no terceiro nível têm a propriedade. A assim por diante para todos os outros níveis.

Em geral, a indução é um método para provar que cada membro de certa coleção de objetos tem uma propriedade. Ela funciona quando (e apenas quando) cada objeto na coleção resulta de alguns “objetos iniciais” por um número finito de iterações de algumas “operações”. No caso de base, demonstra-se que os objetos iniciais têm a propriedade; no passo indutivo, demonstra-se que as operações preservam a propriedades no sentido de que quando uma das operações é aplicada a alguns objetos com a propriedade, o novo objeto resultante tem também a propriedade; e finalmente conclui-se que todos os objetos têm a propriedade.

Essa ideia se manifesta na lógica raras vezes. Uma num estilo de demonstração às vezes chamado “indução sobre construção de fórmula”. Suponha que queremos estabelecer que absolutamente qualquer fbf de LP tenha certa propriedade p. O método de demonstração por indução sobre construção de fórmula nos diz para estabelecer primeiro duas cláusulas:

(B) Toda fbf atômica (i.e., toda letra sentencial) tem a propriedade p.

(I) Para quaisquer fbfs ϕ e ψ, se ambas, ϕ e ψ, têm a propriedade p, então as fbfs ¬ϕ e ϕ → ψ também têm a propriedade p.

Uma vez estabelecidas, a demonstração por indução nos permite concluir que toda fbf tem a propriedade p. Por que essa conclusão é justificada? Lembre-se da definição de fbf […]: qualquer fbf é construída a partir de fbfs atômicas pela aplicação repetida da cláusula (ii): “se ϕ e ψ são fbfs, então ¬ϕ e ϕ → ψ também são fbfs”. Assim, cada fbf é o resultado de um processo finito que começa com fbfs atômicas e continua construindo condicionais e negações das fbfs formadas nos passos anteriores do processo. Mas a cláusula (B) (o caso de base) mostra que os pontos de partida desse processo têm todos a propriedade p. E a cláusula (I) (o passo indutivo) mostra que os passos subsequentes nesse processo preservam a propriedade p: se as fórmulas construídas até então têm a propriedade p, então garante-se que a próxima fórmula no processo (construída de fórmulas anteriores  pelo uso ou da → ou da ¬) também tem p. Assim, todas as fbfs têm a propriedade p. Em termos da ideia geral de demonstração indutiva, as fbfs atômicas são os nossos objetos de partida (assim como os três pontos da base na grade), e as regras da gramática para a ¬ e a → que geram fbf complexas de fbfs mais simples são as operações.

Eis um exemplo simples de demonstração por indução sobre construção de fórmula:

Prove que toda fbf contém um número finito de diferentes letras sentenciais. Estamos tentando provar uma proposição da seguinte forma: toda fbf tem a propriedade p. A propriedade p nesse caso é ter um número finito de diferentes letras sentenciais. A nossa demonstração tem dois passos:

Caso de base: aqui, temos de mostrar que cada fbf atômica – i.e., cada letra sentencial – tem p. Isso é obvio, uma vez que cada letra sentencial contém apenas uma letra sentencial: ela própria.

Passo indutivo: aqui, temos de mostrar que se as fbfs  ϕ e ψ têm a propriedade p, então ¬ϕ e ϕ → ψ também a têm. Comecemos, então, por supor:

as fórmulas ϕ e ψ têm, cada uma, finitamente muitas letras sentenciais diferentes      (HI)

Essa suposição é geralmente chamada de “hipótese indutiva”. Temos então de mostrar que tanto ¬ϕ quanto ϕ → ψ têm finitamente muitas letras sentenciais diferentes. Isso é fácil também. ¬ϕ tem tantas letras sentenciais quanto ϕ; (IH) nos diz que ϕ tem finitamente muitas; ¬ϕ, portanto, tem também finitamente muitas. Já ϕ → ψ tem, no máximo, n + m letras sentenciais, onde n e m são o número de diferentes letras sentenciais em ϕ e ψ respectivamente; (IH) nos diz que n e m são finitos, de modo que n + m é também finito.

Mostramos que toda fórmula atômica tem a propriedade de ter um número finito de letras sentenciais; e mostramos que a propriedade é herdada pelas fórmulas complexas construídas de acordo com as regras de formação. Mas toda fbf é ou atômica, ou construída a partir de fbfs atômicas por uma séria finita de aplicações de regras de formação. Portanto, por indução, todas fbf tem a propriedade.

A seguinte demonstração da correção requer uma forma diferente de demonstração indutiva:

Demonstração da correção de LP. Ao contrário da demonstração anterior, o que estamos tentando provar aqui não tem a forma “Toda fbf tem a propriedade p”. Ao invés, tem a forma “Todo teorema tem a propriedade p”. Ainda podemos usar a indução, mas terá de ser uma indução de um tipo diferente do da indução sobre construção de fórmula. Considere: um teorema é qualquer linha de uma demonstração. E qualquer linha de qualquer demonstração é o resultado de uma série finita de fbfs nas quais cada fbf é ou um axioma, ou se segue de linhas anteriores por MP. Assim, as condições estão certas para uma demonstração indutiva. Os pontos de partida são os axiomas, e a operação é a inferência de uma nova linha a partir de linhas anteriores usando-se MP. Se pudermos mostrar que os pontos de partida (os axiomas) tem a propriedade da validade, e que a operação MP preserve a propriedade da validade, então poderemos concluir que cada fbf em cada demonstração – i.e., todo teorema – tem a propriedade da validade. Esse tipo de demonstração indutiva é chamado de indução “sobre a demonstração de uma fórmula” (ou indução “sobre o comprimento da demonstração da fórmula”).

Caso de Base: aqui, precisamos mostrar que todo axioma de LP é válido. Isso é tedioso, embora simples. Tome LP₁, por exemplo. Suponha por reductio que alguma instância de LP₁ é inválida, i.e., para alguma interpretação ℱ de LP, V_ℱ (ϕ → (ψ → ϕ)) = 0. Assim, V_ℱ (ϕ) = 1 e V_ℱ (ψ → ϕ) = 0. Dado o último, V_ℱ (𝜓) = 1 e V_ℱ (𝜙) = 0; contradição. Pode-se similarmente mostrar que todas as instâncias de LP₂ e LP₃ são também válidas (exercício 2.5).

Passo indutivo: aqui, começamos por supor que cada linha numa demonstração até certo ponto é válida (a hipótese indutiva); temos então de mostrar que adicionando-se outra linha que se segue de linhas anteriores pela regra modus ponens, essa linha tem de ser válida também. Isto é, estamos tentando mostrar que “o modus ponens preserva a validade”. Assim, suponha a hipótese indutiva: que todas as linhas anteriores na demonstração são válidas. E agora, considere o resultado da aplicação do modus ponens. Isso significa que a nova linha que adicionamos à demonstração é alguma fórmula 𝜓 que inferimos de duas linhas anteriores que têm as formas ϕ → ψ e ϕ. Temos de mostrar que 𝜓 é uma fórmula válida, i.e., que é verdadeira em qualquer interpretação. Sendo assim, seja ℱ qualquer interpretação. Pela hipótese indutiva, todas as linhas anteriores na demonstração são válidas, e, por conseguinte, ϕ → ψ e ϕ são válidas. Assim, V_ℱ (ϕ) = 1 e V_ℱ (ϕ → ψ) = 1. Mas se V_ℱ (ϕ) = 1, então V_ℱ (𝜓) não pode ser 0, pois se fosse, então V_ℱ (ϕ → ψ)  seria O, e não é. Portanto, V_ℱ (𝜓) = 1.

(Se o nosso sistema incluísse outras regras além do modus ponens, teria sido necessário mostrar que também preservam a validade. A escassez de regras em sistemas axiomáticos torna a construção de demonstrações naqueles sistemas uma verdadeira chatice, mas vimos agora como deixa a vida metalógica mais fácil).

Mostramos que os axiomas são válidos, e que o modus ponens preserva a validade. Todos os teoremas são gerados a partir dos axiomas via modus ponens numa séria finita de passos. Portanto, por indução, todo teorema é válido.

Q.E. D

A correção nos fornece uma maneira de estabelecer a indemonstrabilidade. A correção diz “se ⊢ ϕ, então ⊨ ϕ”, ou de maneira equivalente: “se ⊭ ϕ, então ⊬ ϕ”. Assim, mostrar que uma fbf não é um teorema, é suficiente para mostrar que não é válido. Considere, por exemplo, (P → Q) → (Q→ P). Essa fbf é falsa numa interpretação de LP na qual P é 0 e Q é 1. Assim, não é válida. Mas então a correção nos diz que também não é um teorema. Em geral: dada a correção, para mostrar que uma fbf não é um teorema, tudo o que você precisar fazer é encontrar uma interpretação na qual ela não seja verdadeira.

Antes de deixarmos esta seção, permitam-me reiterar a distinção entre os dois tipos de indução que são mais comumente usadas na metalógica. A indução sobre a demonstração de uma fórmula (o tipo de indução usada para estabelecer a correção) é usado quando se está estabelecendo um fato da forma: todo teorema certa propriedade p. Aqui, o caso de base consiste em mostrar que os axiomas (LP₁ – LP₃ no caso de LP) têm a propriedade p, e o passo indutivo consiste em mostrar que as regras de inferência preservam p – no caso de LP, que se ϕ e ϕ → ψ tiverem a propriedade p, então ψ também a terá. (As induções sobre demonstrações também podem ser usadas para mostrar que todas as fbf demonstráveis a partir de um dado conjunto Γ têm dada propriedade; nesse caso, o caso de base precisaria incluir uma demonstração de que todos os membros de Γ têm a propriedade). A indução sobre a construção de fórmula (o tipo de indução usada para mostrar que todas as fórmulas têm finitamente muitas letras sentenciais), por outro lado, é usada quando se está tentando estabelecer um fato da forma: toda fórmula tem certa propriedade p. Aqui, o caso de base consiste em mostrar que todas as fbfs atômicas – as letras sentenciais no caso de LP – têm a propriedade p; e o passo indutivo consiste em mostrar que as regras de formação preservam p – no caso de LP, que se e têm a propriedade p, então e também terão a propriedade p.

Se você já provou algo por indução, é importante identificar que tipo de demonstração indutiva está construindo. Com quais entidades você está tratando? Qual é a propriedade p? Quais são os pontos de partida, e quais as operações geram novas entidades a partir dos pontos de partida? Se você estiver tentando construir uma demonstração indutiva e acabar travando, faça essas perguntas e assegure-se de que tem com clareza as respostas.

 

Retirado da seção 2.7, cap. 2. de Logic for Philosophy. Oxford University Press, 2010.

p.s.: as seções 2.8 e 2.9, que tratam do teorema da dedução e da prova de completude para LP, respectivamente, serão publicadas posteriormente.